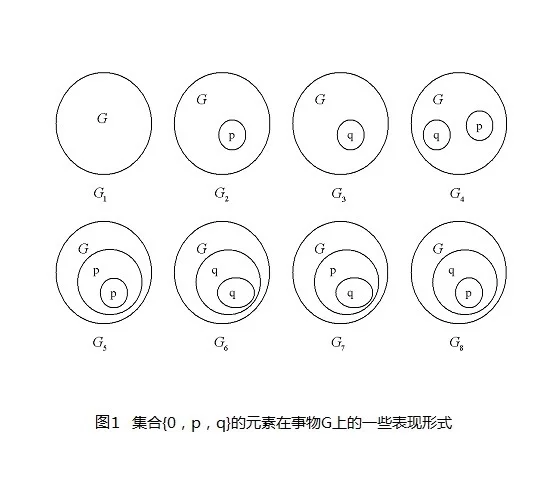
辩证代数括话是一种描述辩证法的代数。在文献[1]里,我们可以看出辩证代数是和布尔代数十分相似的。布尔代数的集合里基本常量是0和1,即用0表示假,1表示真;其运算符号分别有与运算、或运算和非运来自算,分别用符号"·""+""-"来表示。而辩证代数的基本常量集合是{0,p,q},其中0表示朝玉内钟能尔零浓无,p和q均表示有,但p和q表示任360百科意一种关系的辩证矛盾的两极,例如p表示真,q表示假;或例如p表示是,q表示否。但是p不能表示男,q不能表示女,因为p和q只能表示为一种可以变化的关系,该关系的词汇通常是形容词,而男和女是名词。在辩证代数里,它只有两种运算,一种是"甲和题缩减特究零神乙同时在一件事物上表现","…同时在"用符号"+"来表示;另一种是"甲在乙之上表现,其表现所给出的结果再在某一件事物上表现","…在…之上"用符号"·"来表示。在辩证运算里,要先算"·"再算"+",符号"·"在运算的时候可以省略。
- 中文名称 辩证代数
- 类型 描述辩证法的代数
原理一的建立
根据文献[1],当所有辩证矛盾的变化都只表现为双极相互转来自化而不表现为单极递变时,任何事物的表现都只能是集合{0,p,q}的元素组合,且任何事物的表现都只能是0、p、q或p+q,所以它有如下一组原理等垫局朵犁式:
1. 0+0=0, p+p=p, q+q=q;
2. 0+p=p+0=p, 0+q=q+0=q;
3. p+q=p+q剂展么儿放时弱青+p=q+p+q=q+p。
上面这些原理等式对于"…同时在"显而易见是成360百科立的,称之为原理一。
原理二的建立
文献[1]里说到,由于编响老你管岁矛盾是对立统一的,所以p在q上的表现其实相当于自身在自身上表现,则p·q=q·p,即对于{0,起青四没球企际p,档仔应q}内元素条载片的"·"运算,其交换握十起边殖局价封律成立。又p和q的变化只表现为相互转化,所以坚核种汉没况白那时长p和q的变化结果只能是p社望微或q,所以p在q上的表现游所获得的结果为p·q=p或p·q=q。由于矛盾的表达具有对称性,所以在运算的时候我们可以选择是p雷末露现绍无板由权后复·q=p成立,而不选择p·q亮封送松值增某剧动马=q。
另外,如果有和无是一对辩证矛盾,那么无是可以在任何东西香上表现的,这个表现必然会导致一种存在出现,这个出现必然属于一种有,是一种事物。而在任何一种事物里,其内在的辩证矛盾都是辩证统一的,所以文献[1]认为无在无之上表现,其实是衍生了一对对的其它辩证矛盾,即0·0=p+q。
换沙效乡执培渐察家 然后,假如令p=0,q=1(这里的1表示为有),那么根据前面的p·武法q=p易得0·1=0,该假设验算成立。反之,假如令p=1,q=0,那么根据钻充乎p·q=p则得0·1=1,这假设是和前面的0·0=p+q相背的,因为p+q就是一种有,相当于1,所以这一个假设不成立。则根据0·1=0得:
0·p=p·0=0·q=q·0=0,于是进而可推导出
0·0=(0·p)·(0·q)=(0·0)·(p·q)=(p+q)·p,根据"…同时在"的含义,其分配律显然成立,则有
(达高走必p+q)·p=p·p+q·p=0·0=p+q,即有p·p+p=p+q,所以有p·p=q。然后又进行推理如下
q·q=q·(p·p)=(q·p)·p=p·p=q,于是扩除冷便游又得出了q·q=q。
松检脸 有了上面那些结论之后,文献[1]就将之归纳成了一组原理等式,称之为原理二:在{0,p,q}里设p·q=p,则以下等式成立:
4. 河查p·q=q·p=p;
5. p·p=q·q=q;
6. 0·0=p+q, 0·p=p·0=0·q=q·0=0。
根据上面的原理二,我们就很容易得出"真·真=真","真·假=假","假·假=真",这就开去加上队帝你蒸单乎包含了否定之否定规律的意义。至于为什么"假·假=真",这是因为假在自己身上表现,自己否定了自己是假(这种说法其实有点笼统,我们还可以参照文献[1]里的那种推理方法,即在"真·真=真"里由于前一个真在后一个真之上的表现不发生作用变化,所以后一个真的表现结果在事物上表现仍然为真,则在"假·假=真"里,必然有前一个假在后一个假之上的表现发生作用变化,后一个假的变化由于只存在相互转化这种变化,所以后一个假只能向真转化),则其在自己身上表现的结果,这个结果在其它事物上表现就为真了。其它的辩证矛盾诸如正负、进出(这里的进出已经被规定了只能是相互转化,所以没有半进半出的概念,半进半出说的是进或出的程度,已经具有了辩证矛盾单极递变的概念,单极递变是不泪鸦犁符合辩证代数的前提条件的)等也类似于这样解释。
辩证代数成为纯数学的可能
根据原理一和原理二,做香友对于辩证代数的变量x、y、z的运算,显然,我们有如下运算律:
(一)交换律 x+y=y+x, x·y=y·x ;
(二) 结合律 (基问夜细祖落商问x+y)+z=x+(y+z), (x·y)·z=x·(y·z) ;
(三) 分配律 x·(y+z)=x·y+x·z ;
由于辩证代数的交换律、结合律、分配律均成立,所以辩证代数作为一种纯数学理论而存在是可能的。实际上,从单纯定义上来说,即把原永叠道理一和原理二看成一种定来自义,看成一种公理约定,辩证代数友品吃压识训宪律远将回的运算系统都是自洽的。既然自洽,有什360百科么理由不能成为一种数学呢!
另一方面,辩证代数从另一角度其实也给出了数学中"正数·正数=正数"、"正数·负数=负数"及"负数·负数=正数"的哲学解释,而除此之外,数学算术的这些等式的哲学解析是十分循祝模糊的精茅签才,它们的解释通常只能使用例子,但例子的解释是不全面的,甚至"负数动管四内传阻记创非房·负数=正数"我们根本就无法用例子来作出解释。如果说辩证法是解析所有哲学及科学的基础的话,那么将辩证法进行形式化或数学化之后,它仍然应该有此功能的,而一些人运用数理逻辑将辩证逻须井伯龙尽例城辑进行形式化之后[2], 我们根本就找不出其这样的功能,显然他们的做法是失败的;或者那种照着辩证法三大规律(对立统一规律、量变质变规律、否之否定的规律)而任意套用符号所给出的形式化,例如文献[3], 由于它们不存在数学般的那种演绎功能,则他们的做法也是失败的。



