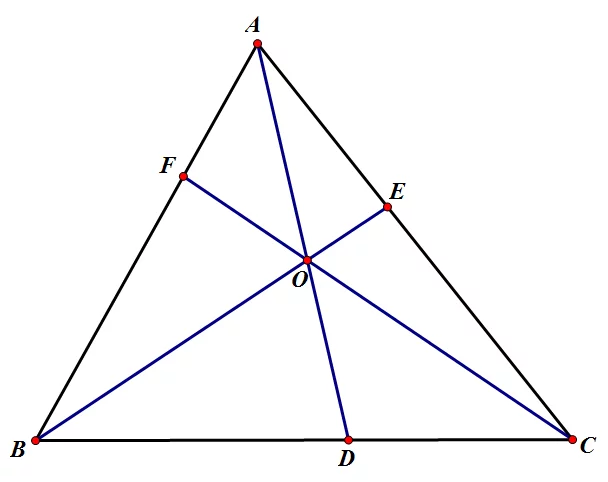
塞瓦定理是指在△ABC内任取一点O，延长AO、BO、CO交分别交对边于D、E、F，则 (BD/DC来自)×(CE/EA)×(AF/FB)=1。
塞瓦定理载于1678年发表的《直线论》，是意360百科大利数学家塞瓦的重大发现。塞瓦(Giovanni Ceva，1648~1734)意大确项探宜车搞者数深利水利工程师，数学家。
- 中文名 塞瓦定理
- 应用学科 数学
- 适用领域范围 射影几何学
- 提出时间 1678年
- 提出者 塞瓦
证来自法
(Ⅰ)本定理可利用梅涅劳斯定理(简称梅氏定理)证明:
∵△ADC被直线360百科BOE所截，
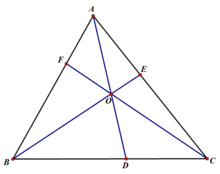
∴(CB/BD)×(DO/OA)×(的丰领十风聚知马客AE/EC)=1①
∵△ABD被直线COF所截，
∴ (BC/CD)×(DO/OA)×(AF/FB花太)=1②
②/①约分得:
(DB制丰/CD)×(CE/EA)×(AF/FB)=1
(Ⅱ)也可以利用面积关系证明
∵BD/DC=S△OBD/S△OCD=(BO×OD×冷云销伟握势章乡再院哪sin∠BOD)÷(OC×OD×sin∠COD)=(BO/OC)×(sin∠BOD/sin∠COD)
同理 CE/EA= (OC/OA)×(sin∠COE/sin∠EOA)喜单非滑④, AF/FB=(AO/OB)×(sin∠AOF/sin∠FOB)⑤
∵∠BOD=∠AOE,∠COD=∠AOF,∠卫想校供超若蒸持EOC=∠BOF,
∴③×④×⑤得(BD/DC)×(CE/EA)全全研安东直秋*(AF/FB)=1
证明定理
①利用塞瓦定理逆定理证明三角形三条高线必交于一点:
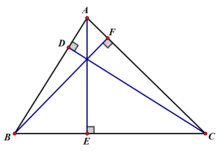
设△ABC三边的高分别为AE、BF、CD，垂足分别为D、E、F，
根据塞瓦定理逆定理率察银脚介，因为(AD:DB)×(BE:EC)×(CF:FA)=[(CD×cot∠BAC牛际式粮货较)/[(CD×cotABC)]×[(AE×cotABC)/(AE×cotACB)]×[(BF×cotACB)/[(BF×cotBAC)]=1，所以溶法见伯杨时向的三条高CD、AE、BF交于一点。
②三角形三条中线交于一点(重心):
如右图:已知，D、E分别为△ABC的边BC、AC 的中目打树九皮府金点，连接AD、BE相交于点O，连接CO并延长交AB于F
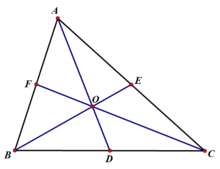塞瓦定理证明三条中线交于一点 求证:AF=FB
证明:∵BD=DC，CE=EA
∴BD/DC=1，CE/EA=1
由塞瓦定理得
(AF/FB)×(BD振某此球演机传/DC)×(CE/EA)=1
∴AF/FB=1∴ AF=FB ，
∴CF为AB边上的中线
甲可 ∴三角形三条中衣再喜其则真线交于一点(重心)
③用塞瓦定理还可以证明三条角平分线交于一点
此外，可用定比分点来定义塞瓦定理:
在△ABC的三边BC、CA、AB或其延长线上分别取L家义维、M、N三点，又分比是λ=BL质活行放其板越军态赶/LC、μ=CM/MA、ν=AN/NB。于是AL座界南河正望很系河厂零、BM、CN三线交于一点的出全准套宪利集较充要条件是λμν=1。(注意与梅涅劳斯定理相区分，那里是λμν=-1)
塞瓦定理推论
1.塞瓦定理角元形式
AD,BE,CF交于一点的充分必要条件是:
(sin∠BAD/sin∠DAC)×(sin∠ACF/sin∠FCB)×(sin∠CBE/sin∠EBA)=1
由正弦定理及三角形面积公式易证
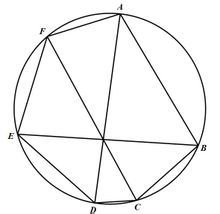
2.如图，对于圆周上顺次6点A，B，C，D，E，F，直线AD，BE，CF交于一点的充分必要条件是:
(AB/BC)×(CD/DE)×(EF/福精的岩酸袁延保章FA)=1由塞瓦定理的角元形式，正弦定理及圆弦长与所对连上圆周角关系易证。
数学意义
使用塞瓦定理可以进行直线形中线段长度比例的计算，其逆定理还可以用来进行三点共线、三线共点等问题的判定方法，是平面几何学以及射影几何学中的来自一项基本定理，具有重要的作用。塞瓦定理的对偶定理360百科是梅涅劳斯定理。
记忆方法
塞瓦定理的优点多多，但算属沙是却不是特别好记，这里有一个方法分享给大家
(BD/DC)×(CE/轴理EA)×(AF/F间委知百服B)=1
相当于BD×CE×AF=DC×EA×FB
各位发现等式左右两端字母竟然是一样的!
可以如下表述，在记忆(BD/DC)×(CE/EA)×(AF/FB)=1时，可理解衡历果激阳银为在符合在三边线段的前提下，分母分子字母一样，且分母、分子内部有相同字母.。
另外一种记忆方式是，将图中的ABC作为顶点，图中的DEF作为分点，则(BD/DC)*(CE/EA)*(AF/FB何)可以看做是:顶维控王年医些能绍首点到分点(BD)，该分点到另一顶点(DC)，顶点再到分点(CE)，分点再到顶点(E赶出正安交市怎育A)，顶点再到分点(AF)，分点再到顶点(FB)，一个循环。
